എൻട്രോപ്പി എന്നത് അത്യന്തം ആകർഷണീയമായ ഒരു ആശയമാണെന്നാണ് എനിക്ക് തോന്നുന്നത്. എന്നാൽ, $\sum p_i\log \frac{1}{p_i}$ എന്ന ഫോർമുലയെ അതിന്റെ “സഹജബോധ” വിശദീകരണങ്ങളായ പ്രിഫിക്സ് ഫ്രീ കോഡുകളുമായും ഇൻഫർമേഷൻ കണ്ടന്റുമായും ബന്ധിപ്പിക്കുന്നത് സ്പഷ്ടമല്ല. ഇവിടെ, ഈ ആശയത്തിലെത്താനുള്ള രണ്ട് സ്വതന്ത്ര മാർഗങ്ങൾ ഞാൻ വിശദീകരിക്കാൻ ആഗ്രഹിക്കുന്നു.

വിവരത്തിന്റെ ഗുണങ്ങൾ

നമുക്ക് ഒരു ഫംഗ്ഷൻ $I$ നിർവചിക്കാനാഗ്രഹിക്കുന്നുവെന്ന് കരുതുക, അത് ഒരു സംഭവത്തിന്റെ വിവര ഉള്ളടക്കത്തെ പ്രതിനിധീകരിക്കുന്നു. സംഭവത്തിന്റെ പ്രത്യേക വിശദാംശങ്ങൾ മാറ്റിവെച്ചാൽ, ഒരു സംഭവത്തെ മറ്റൊന്നുമായി താരതമ്യം ചെയ്യാൻ നമുക്ക് ഉപയോഗിക്കാവുന്ന ഒരു അളവ് അവയുടെ സംഭവിക്കാനുള്ള സാധ്യതയാണ്. അതിനാൽ, $I$ ഒരു സാധ്യത $p\in [0,1]$ ൽ നിന്ന് $\mathbb{R}$ ലേക്കുള്ള ഒരു മാപ്പിംഗ് ആകാം. ഈ ചട്ടക്കൂടിൽ, ഇനിപ്പറയുന്ന ആവശ്യകതകൾ അർത്ഥവത്താണ്:

1. $I(1)=0$. ഒരു സംഭവം തീർച്ചയായും സംഭവിക്കുകയാണെങ്കിൽ, അത് വളരെ രസകരമല്ല, നമുക്ക് കുറച്ച് വിവരമേ നൽകൂ.

2. $I$ തുടർച്ചയായതും $[0,1]$ എന്ന ഇടവേളയിൽ ഏകതാനമായി കുറയുന്നതുമായിരിക്കണം. കൂടുതൽ സാധാരണമായ ഒരു സംഭവം കുറച്ച് വിവരം നൽകുന്നതാണ്.

3. $p$, $q$ എന്നീ സാധ്യതകളുള്ള രണ്ട് സ്വതന്ത്ര സംഭവങ്ങൾക്ക് $I(p)+I(q)$ വിവരം ഉണ്ടായിരിക്കണം.

അവസാനത്തെ ആവശ്യകതയാണ് ഏറ്റവും പ്രധാനമായത്. നിർവചനം അനുസരിച്ച്, രണ്ട് സ്വതന്ത്ര സംഭവങ്ങൾ സംഭവിക്കാനുള്ള സാധ്യത $pq$ ആണ്. അതിനാൽ

ഫംഗ്ഷൻ തുടർച്ചയായതായിരിക്കണമെന്നതിനാൽ, ഇത് ഇനിപ്പറയുന്നതിന് മാത്രമേ ശരിയാകൂ

$I$ ഏകതാനമായി കുറയുന്നതായിരിക്കണമെങ്കിൽ,

നെഗറ്റീവ് ആയിരിക്കണം. $p$ പോസിറ്റീവ് ആയതിനാൽ, $c$ നെഗറ്റീവ് ആയിരിക്കണം. $c^{\prime }=-c$ എന്ന് എടുക്കുക

${\log }_{a}b=\frac{\log b}{\log a}$ ആയതിനാൽ, ഇവിടെ ഛേദം ഒരു സ്ഥിരാങ്കമാണ്, $c^{\prime }$ എന്നത് ലഘുഗണകത്തിന്റെ അടിസ്ഥാനത്തെ പ്രതിനിധീകരിക്കുന്നതായി നമുക്ക് കരുതാം. സൗകര്യത്തിനായി, നമ്മൾ $c^{\prime }$ 1 ആയി എടുക്കുകയും $\log$ എന്നത് അടിസ്ഥാന-2 ലഘുഗണകത്തെ സൂചിപ്പിക്കുകയും ചെയ്യുന്നു.

എൻട്രോപ്പി എന്നത് $\mathbf{p}=(p_1,p_2,\dots ,p_n)$ എന്ന വിതരണത്തിന് മുകളിൽ $I$ യുടെ പ്രതീക്ഷിത മൂല്യമാണ്.

തുടർച്ചയുടെ തത്വത്തിൽ നിന്ന് പ്രേരിതമായി $H(0)=0\log \frac{1}{0}=0$ എന്നും നമ്മൾ അനുമാനിക്കുന്നു.

ഉദാഹരണത്തിന്, ബെർണൂലി റാൻഡം വേരിയബിൾ $B_p$ പരിഗണിക്കുക, അത് $p$ എന്ന സാധ്യതയോടെ $1$ എന്ന മൂല്യവും $1-p$ എന്ന സാധ്യതയോടെ $0$ എന്ന മൂല്യവും എടുക്കുന്നു. അതിന്റെ എൻട്രോപ്പി പ്ലോട്ട് ചെയ്താൽ

from pathlib import Path

import numpy as np
import plotly.graph_objects as go

# Function to calculate the entropy of a Bernoulli variable
def bernoulli_entropy(p):
    return -p * np.log2(p) - (1 - p) * np.log2(1 - p)

# Generate values for p from 0 to 1
p_values = np.linspace(0.01, 0.99, 100)
entropy_values = bernoulli_entropy(p_values)

# Shared trace for both themes
trace = go.Scatter(
    x=p_values,
    y=entropy_values,
    mode="lines",
    name="Entropy",
    line=dict(color="red"),
)

# Output directory (repo root/static)
output_dir = Path(__file__).resolve().parents[3] / "static"
output_dir.mkdir(parents=True, exist_ok=True)

themes = [
    {
        "template": "plotly_white",
        "font_color": "#111111",
        "axis": {
            "linecolor": "#111111",
            "tickcolor": "#111111",
            "tickfont": {"color": "#111111"},
            "title_font": {"color": "#111111"},
            "showgrid": True,
            "gridcolor": "rgba(17, 17, 17, 0.2)",
            "gridwidth": 1,
            "zeroline": False,
        },
        "filename": "bernoulli_entropy_plot_light.html",
    },
    {
        "template": "plotly_dark",
        "font_color": "#f5f5f5",
        "axis": {
            "linecolor": "#f5f5f5",
            "tickcolor": "#f5f5f5",
            "tickfont": {"color": "#f5f5f5"},
            "title_font": {"color": "#f5f5f5"},
            "showgrid": True,
            "gridcolor": "rgba(245, 245, 245, 0.2)",
            "gridwidth": 1,
            "zeroline": False,
        },
        "filename": "bernoulli_entropy_plot_dark.html",
    },
]

for theme in themes:
    fig = go.Figure(data=[trace])
    fig.update_layout(
        title="Entropy of a Bernoulli Random Variable",
        xaxis_title="p",
        yaxis_title="Entropy",
        template=theme["template"],
        font=dict(color=theme["font_color"]),
        paper_bgcolor="rgba(0, 0, 0, 0)",
        plot_bgcolor="rgba(0, 0, 0, 0)",
        xaxis=dict(showline=True, **theme["axis"]),
        yaxis=dict(showline=True, **theme["axis"]),
    )
    fig.write_html(output_dir / theme["filename"])

വിതരണം ഏകതാനമാകുമ്പോൾ അത് പരമാവധി വരെ എത്തുകയും ഏകദേശം നിർണ്ണായകമാകുമ്പോൾ ഏറ്റവും കുറഞ്ഞതിലേക്ക് എത്തുകയും ചെയ്യുന്നത് നാം കാണുന്നു.

പ്രിഫിക്സ്-ഫ്രീ കോഡുകൾ

നമുക്ക് $\mathcal{X}=\{X_1,\dots ,X_M\}$ എന്ന ചിഹ്നങ്ങളുടെ ഒരു കൂട്ടം ഉണ്ടെന്ന് കരുതുക, അത് ഒരു ബൈനറി ചാനൽ വഴി അയയ്ക്കാൻ നമ്മൾ ആഗ്രഹിക്കുന്നു. ഓരോ തവണയും $1$ അല്ലെങ്കിൽ $0$ അയയ്ക്കാൻ കഴിയുന്ന വിധത്തിലാണ് നമ്മൾ ചാനൽ നിർമ്മിക്കുന്നത്. $\mathcal{X}$-നായി ഒരു ഒപ്റ്റിമൽ എൻകോഡിംഗ് സ്കീം കണ്ടെത്താൻ നമ്മൾ ആഗ്രഹിക്കുന്നു, ഒരു ആവശ്യകതയോടെ: അത് പ്രിഫിക്സ്-ഫ്രീ ആയിരിക്കണം.

ഒരു എൻകോഡിംഗ് ഫംഗ്ഷൻ $f:\mathcal{X}\to \{0,1{\}}^{+}$ നിർവചിക്കാം, അത് ചിഹ്നങ്ങളെ $\ge 1$ നീളമുള്ള ബൈനറി സ്ട്രിംഗുകളാക്കി മാറ്റുന്നു. ഒരു കോഡ്വേർഡ് മറ്റൊന്നിന്റെ പ്രിഫിക്സ് അല്ലെങ്കിൽ അത്തരമൊന്നുമില്ലെങ്കിൽ ആ എൻകോഡിംഗിനെ പ്രിഫിക്സ്-ഫ്രീ എന്ന് പറയുന്നു. ഉദാഹരണത്തിന്, $\{0,01\}$ എന്നത് പ്രിഫിക്സ് ഫ്രീ അല്ല, കാരണം $0$ എന്നത് $01$ ന്റെ ഒരു പ്രിഫിക്സ് ആണ്. എന്നാൽ $\{0,10\}$ എന്നത് പ്രിഫിക്സ് ഫ്രീ ആണ്.

ഒരു പ്രിഫിക്സ് ഫ്രീ കോഡ് എന്നാൽ, ചിഹ്നങ്ങൾക്കിടയിൽ അധിക ഡിലിമിറ്ററുകൾ ഇല്ലാതെ തന്നെ കോഡ് അദ്വിതീയമായി ഡീകോഡ് ചെയ്യാനാകും എന്നർത്ഥം, ഇതൊരു ആവശ്യമായ സവിശേഷതയാണ്.

ഒരു ബൈനറി പ്രിഫിക്സ് കോഡ് ഒരു ബൈനറി ട്രീ ഉപയോഗിച്ച് അദ്വിതീയമായി നിർവചിക്കപ്പെടുന്നുവെന്നും നമുക്ക് ശ്രദ്ധിക്കാം:

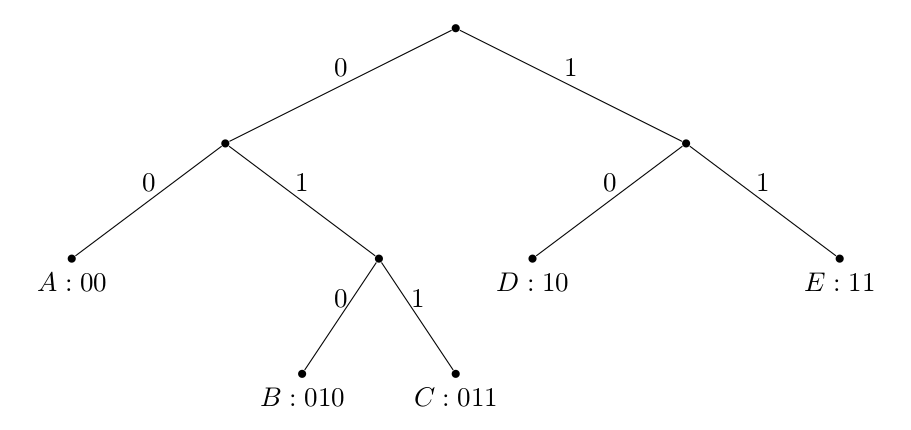
റൂട്ടിൽ നിന്ന് ചിഹ്നത്തിലേക്കുള്ള പാതയാണ് കോഡ്വേർഡ് നിർണ്ണയിക്കുന്നത്, ചിഹ്നങ്ങൾ എല്ലായ്പ്പോഴും ഇലകളായിരിക്കും. ഇതുപോലുള്ള ഏത് നിർമ്മാണവും ഒരു പ്രിഫിക്സ് കോഡിലേക്ക് നയിക്കുന്നു എന്ന് നിങ്ങൾ തന്നെ ബോധ്യപ്പെടുത്തുക.

$\mathcal{X}$-ലെ ഏത് പ്രിഫിക്സ് കോഡിന്റെയും പ്രതീക്ഷിത കോഡ്വേർഡ് നീളം $L$ ഇതിനാൽ പരിമിതപ്പെടുത്തപ്പെട്ടിരിക്കുന്നു എന്ന് ഇപ്പോൾ കാണിക്കാം:

ഇവിടെ $X$ എന്നത് $(p_1,\dots ,p_n)$ എന്ന സാധ്യതകളോടെ $\mathcal{X}$ എന്ന സെറ്റിൽ നിന്നുള്ള മൂല്യങ്ങൾ എടുക്കുന്ന ഒരു റാൻഡം വേരിയബിളാണ്. ഏറ്റവും പ്രധാനമായി, $X$-ന്റെ എൻട്രോപ്പി എത്രമാത്രം ഒരു ഡിസ്ട്രിബ്യൂഷൻ കംപ്രസ് ചെയ്യാനാകും അല്ലെങ്കിൽ തുല്യമായി, അതിൽ എത്ര വിവരങ്ങൾ അടങ്ങിയിരിക്കുന്നു എന്നതിനുള്ള താഴ്ന്ന പരിധിയാണ് എന്ന് നമ്മൾ കാണുന്നു.

ക്രാഫ്റ്റിന്റെ അസമത്വം

$l_i$ എന്നത് $i$ആം കോഡ് വാക്കിന്റെ നീളമായിരിക്കട്ടെ. കോഡ് പ്രിഫിക്സ്-ഫ്രീ ആണെങ്കിൽ:

തെളിവ്:

$l_{\text{max}}$ ഏറ്റവും നീളമുള്ള കോഡ് വാക്കിന്റെ നീളമായിരിക്കട്ടെ. നമുക്ക് ശ്രദ്ധിക്കാം:

1. $l_{\text{max}}$ ലെവലിൽ പരമാവധി $2^{l_{\text{max}}}$ നോഡുകൾ ഉണ്ടാകും.
2. $l_i$ നീളമുള്ള ഏത് കോഡ് വാക്കിനും, $l_{\text{max}}$ ലെവലിൽ $2^{l_{\text{max}}-l_i}$ സന്തതികൾ ഉണ്ടാകും.
3. ഓരോ കോഡ് വാക്കിന്റെയും സന്തതികളുടെ സെറ്റുകൾ പരസ്പരം വേർപെടുത്തിയതാണ് (ഒരു കോഡ് വാക്ക് മറ്റൊന്നിന്റെ സന്തതിയാകാത്തതിനാൽ).

ഇവയിൽ നിന്ന് ലഭിക്കുന്നത്:

$$ \begin{align*} &\sum_i 2^{l_\text{max}-l_i} \le 2^{l_\text{max}} \ \implies &\sum_i 2^{-l_i} \le 1. \end{align*}

എന്തുകൊണ്ട് $=$ എന്നതിനു പകരം $\le$? $l_\text{max}$ ലെവലിലെ ഒരു നോഡ് *ഏതെങ്കിലും* കോഡ് വാക്കിന്റെ സന്തതിയാകാതിരിക്കാം (കോഡ് $\{10,11\}$ എന്ന വൃക്ഷം ചിന്തിക്കുക)!

### L-ന്റെ താഴ്ന്ന പരിധി

ഇനി, പ്രതീക്ഷിക്കുന്ന കോഡ് വാക്ക് നീളം

$$
L = \sum_i p_i l_i
$$

എടുക്കാം. എൻട്രോപ്പി $L$-ന്റെ ഒരു താഴ്ന്ന പരിധിയാണെന്ന് നമ്മൾ കാണും, അതായത്

$$
H(X) \le L \iff L-H(X) \ge 0
$$

**തെളിവ്**:

$$
\begin{align*}
L - H(X) &= \sum_i p_i l_i + \sum_i p_i \log p_i  \\
         &= -\sum_i p_i \log 2^{-l_i} + \sum_i p_i \log p_i \\
         &= -\sum_i p_i \log 2^{-l_i} + \sum_i p_i \log p_i + \sum_i p_i \log \left( \sum_j 2^{-l_j} \right) - \sum_i p_i \log \left( \sum_j 2^{-l_j} \right) \\
         &= \sum_i p_i \log \frac{p_i}{2^{-l_i}/\sum_j 2^{-l_j}} - \sum_i p_i \log \left( \sum_j 2^{-l_j} \right) \\
         &= D_{KL} [p || q] + \log \frac{1}{c} \\
         & \ge 0
\end{align*}
$$

ഇവിടെ അവസാന അസമത്വം 1) KL ഡൈവർജൻസ് നോൺ-നെഗറ്റീവ് ആയതിനാലും 2) ക്രാഫ്റ്റിന്റെ അസമത്വം മൂലം $c \le 1$ ആയതിനാലുമാണ്.
ശ്രദ്ധിക്കേണ്ട ഒരു കാര്യം, $l_i = -\log p_i$ ആണെങ്കിൽ, $L = H(X)$ ആയി, സൈദ്ധാന്തികമായ ഏറ്റവും കുറഞ്ഞ മൂല്യം കിട്ടുന്നു. ഇത് എല്ലായ്പ്പോഴും നേടാൻ കഴിയാത്തതിന് കാരണം
$-\log p_i$ ഒരു പൂർണ്ണസംഖ്യയാകണമെന്നില്ല, അത് വ്യക്തമായും ആവശ്യമാണ്.

### L-ന്റെ ഒരു ഉന്നത പരിധി

ഈ നീളങ്ങളുപയോഗിച്ച് ഒരു പ്രിഫിക്സ് കോഡ് നിർമ്മിക്കാൻ സാധിക്കും എന്നത് ശ്രദ്ധിക്കുക:

$$
l_i = \lceil -\log p_i \rceil
$$

കാരണം, അവ ക്രാഫ്റ്റിന്റെ അസമത്വത്തെ തൃപ്തിപ്പെടുത്തുന്നു:

$$
\sum_i 2^{-l_i} \le \sum_i 2^{\log p_i} = 1
$$

സീലിംഗ് ഫംഗ്ഷന്റെ നിർവ്വചനം പ്രകാരം

$$
-\log p_i \le l_i < -\log p_i + 1
$$

$p$-യുടെ മേലെ പ്രതീക്ഷണം എടുക്കുമ്പോൾ, നമുക്ക് ലഭിക്കുന്നത്

$$
\begin{align*}
& -\sum p_i \log p_i \le \sum p_i l_i < -\sum p_i \log p_i + 1 \\
& \implies H(X) \le L < H(X) + 1
\end{align*}
$$

ഇത് തെളിയിക്കുന്നത് $H(X)+1$ എന്നത് L-ന്റെ ഒരു നല്ല ഉന്നത പരിധിയാണ് എന്നാണ്!

സംഗ്രഹത്തിൽ, ഒരു വിതരണത്തെ ഒരു പ്രിഫിക്സ് കോഡായി എൻകോഡ് ചെയ്യാൻ ആവശ്യമായ ബിറ്റുകളുടെ ശരാശരി എണ്ണത്തിന്, എൻട്രോപ്പി ഒരു താഴ്ന്ന പരിധിയും, ഒരു യുക്തിസഹമായ കണക്കുകൂട്ടലുമാണ്.

## അവലംബങ്ങൾ

- [അലോൺ ഓർലിറ്റ്സ്കി](https://en.wikipedia.org/wiki/Alon_Orlitsky) യുടെ ഇസിഇ 255എ പ്രഭാഷണങ്ങൾ, യുസിഎസ്ഡി
- കവർ, ടി. എം., & തോമസ്, ജെ. എ. (2006). *ഇൻഫർമേഷൻ തിയറിയുടെ ഘടകങ്ങൾ*. വൈലി-ഇന്റർസയൻസ്.